56juqingba.com – What's Your Question?

Compound interest differs from simple interest because it allows you to earn interest not only on your initial investment (the principal) but also on the interest that has already accumulated. This causes accounts with compound interest to grow at a faster rate than those with simple interest. For instance, if your interest compounds annually, you’ll earn more interest in the second year than you did in the first, as the interest accumulates on both the principal and the interest already earned. Moreover, the growth rate accelerates even further if the interest is compounded multiple times per year. Compound interest is commonly applied to a range of investment products and can also be charged on certain loans, such as credit card debt.

To calculate the growth of an investment under compound interest, you can use specific mathematical formulas. For more details on compound interest and how it works, you can visit Investopedia’s compound interest guide.

Compound Interest Formula

The fundamental formula for calculating compound interest is: FV=P(1+ic)n⋅cFV = P \left(1 + \frac{i}{c}\right)^{n \cdot c}

In this formula, “FV” represents the future value of the investment, “P” is the principal or initial amount, “i” is the annual interest rate, “c” is the number of times interest is compounded per year, and “n” is the number of years the investment will grow.

Part1

Finding Annual Compound Interest

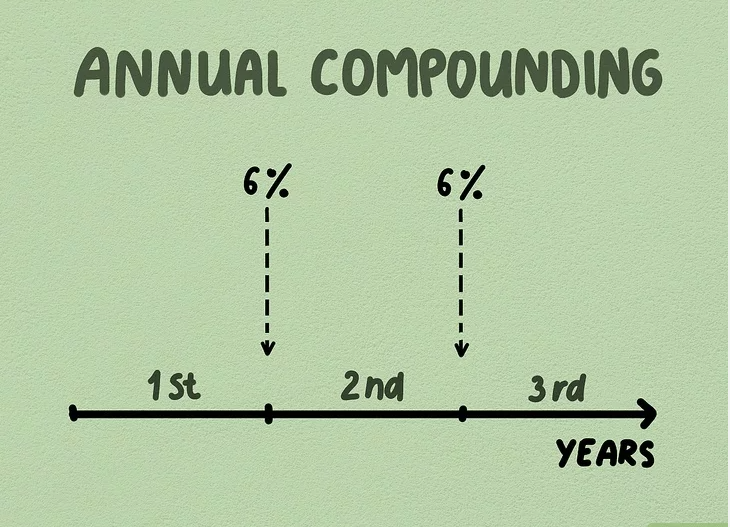
1. Define annual compounding. The interest rate shown on your investment or loan agreement is typically expressed as an annual rate. For example, a 6% car loan means you pay 6% interest each year. When interest compounds annually, it is calculated just once at the end of the year, making it the simplest form of compound interest.

Debt can compound interest in different ways, such as annually, monthly, or even daily. The more frequent the compounding, the faster the interest accumulates. From the investor’s perspective, frequent compounding means greater interest earnings, while for a debtor, it means higher interest payments. For example, a savings account might compound interest annually, while payday loans may compound monthly or weekly.

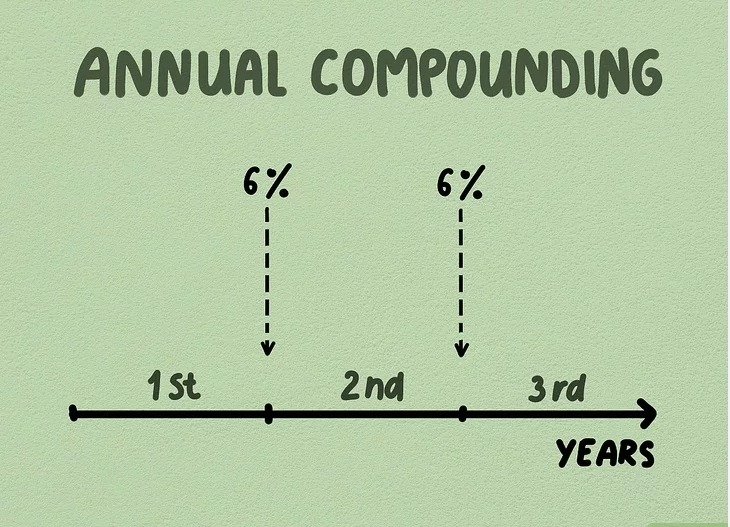
2. Calculate interest compounding annually for year one. Assume you hold a $1,000, 6% savings bond issued by the US Treasury. Treasury savings bonds pay out interest each year based on the bond’s value and interest rate. In year one, the interest would be $60 ($1,000 × 6% = $60).

To calculate the interest for the second year, add the original principal to the interest earned so far. In this case, the principal for year two becomes $1,060 ($1,000 + $60). Interest for year two will be calculated based on this new amount, $1,060.

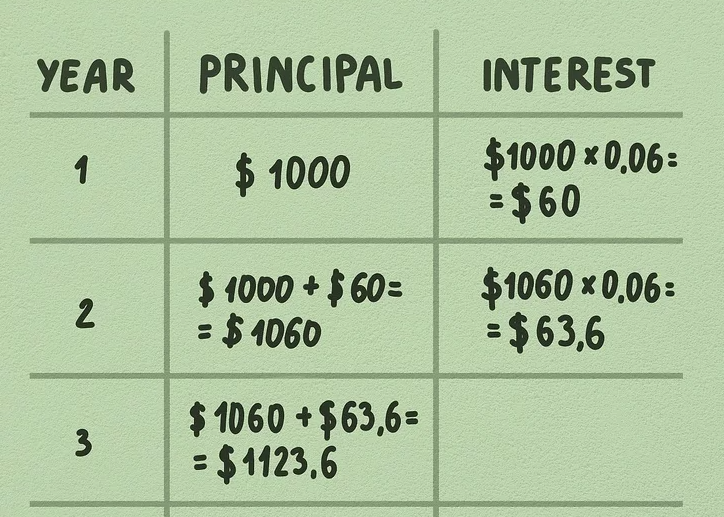
3. Compute interest compounding for later years. To understand the impact of compound interest, you need to calculate the interest for subsequent years. As each year passes, the principal continues to grow. For example, in year two, multiply the new principal ($1,060) by the bond’s interest rate (6%): $1,060 × 6% = $63.60. This is $3.60 more than the previous year’s interest because the principal increased from $1,000 to $1,060.

For year three, the new principal is $1,123.60 ($1,060 + $63.60). The interest earned for year three will be $67.42. This amount is then added to the principal for the year-four calculation. As time passes, the effects of compound interest become more pronounced.

Without compounding, you would earn simple interest, where each year’s interest is calculated only on the original principal. For example, with simple interest, the year-two interest would be just $60 ($1,000 × 6%).

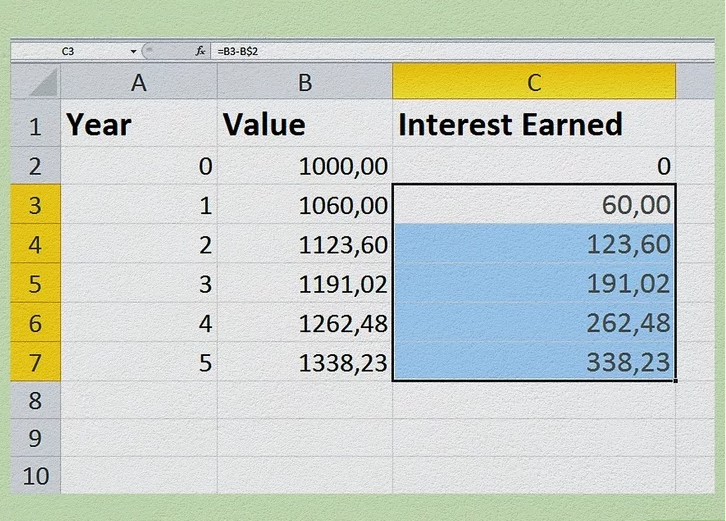
4. Create an Excel document to compute compound interest. A simple way to visualize the growth of your investment is by creating an Excel model. Start by opening a new document and label the columns as “Year,” “Value,” and “Interest Earned.”

In column A (cells A2 to A7), enter the years (0-5). In column B, input the principal amount in cell B2 (e.g., $1,000). For year two (cell B3), enter the formula =B2*1.06 and press enter. This formula assumes the interest is compounded annually at 6%. Drag the formula down to fill the cells down to B7, and Excel will automatically calculate the values.

In column C, start by entering 0 in cell C2. Then, for cell C3, input the formula =B3-B$2 to calculate the interest earned by subtracting the initial principal from the value. Drag this formula down to fill the remaining cells in column C.

This Excel model will track your investment growth over time and can easily be adjusted by changing the principal or interest rate. For a deeper understanding of compound interest, visit Investopedia’s compound interest guide.

2.Calculating Compound Interest on Investments

1. Learn the compound interest formula. The compound interest formula is used to calculate the future value of an investment over a set number of years. The standard formula is: FV=P(1+ic)n⋅cFV = P \left(1 + \frac{i}{c}\right)^{n \cdot c}

Where:

• “FV” is the future value, which is the result of the calculation.
• “P” represents the principal (initial investment).
• “i” is the annual interest rate.
• “c” is the compounding frequency (how many times interest is compounded each year).
• “n” is the number of years the investment will grow.

Alternatively, for a quicker method, you can use the continuous compounding formula, which calculates the maximum future value of an investment by assuming an infinite number of compounding periods. The formula for continuous compounding is: FV=PV⋅ei⋅tFV = PV \cdot e^{i \cdot t}

Where:

• “FV” is the future value of the investment.
• “PV” is the present value (principal).
• “e” is Euler’s number (approximately 2.71828).
• “i” is the interest rate.
• “t” is the time in years.

For more details on compound interest formulas, visit Investopedia’s guide on compound interest.

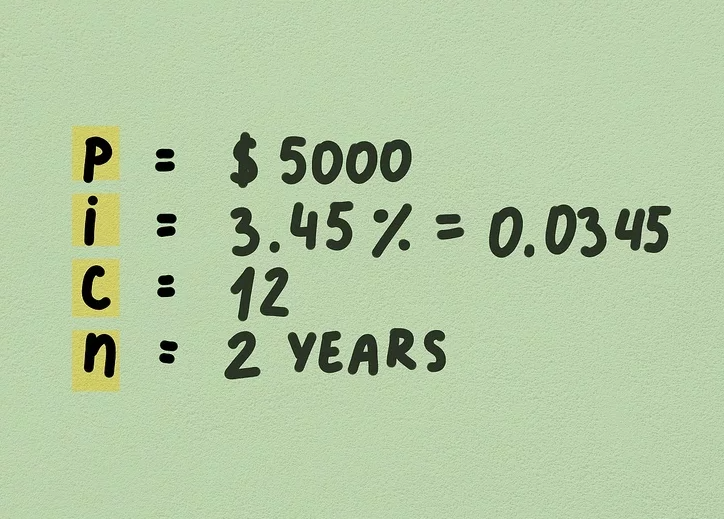
2. Gather the variables for the compound interest formula. Before using the compound interest formula, you need to gather certain information. This includes:

• The principal amount, which is your initial investment (e.g., $5,000).
• The interest rate, usually expressed annually as a percentage. For example, a 3.45% interest rate would be written as 0.0345 in decimal form.
• The compounding frequency (how often interest compounds per year). For example, if interest compounds monthly, the frequency (“c”) would be 12.
• The time period for which the interest is to be calculated (in years). For example, let’s assume you’re measuring over 2 years.

To convert the interest rate into decimal form, divide it by 100. For example, 3.45% becomes 0.0345.

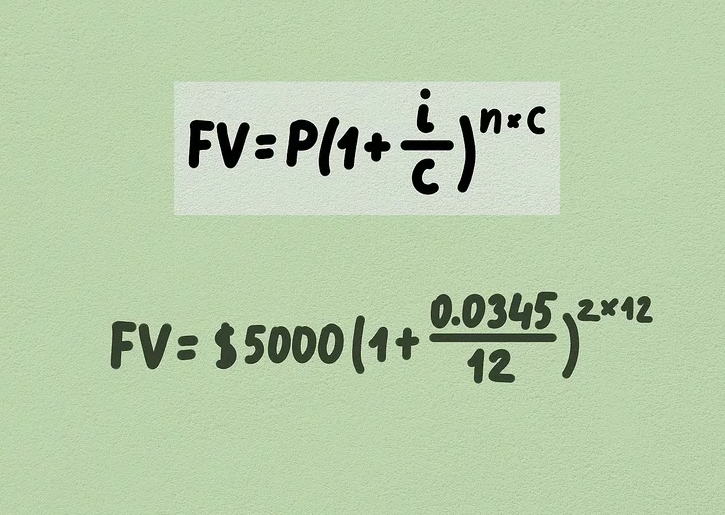
3. Use the formula to calculate compound interest. Once you’ve gathered all the necessary variables, input them into the formula. For example, if your investment is $5,000 with a 3.45% interest rate compounded monthly for 2 years, the formula would look like: FV=5000(1+0.034512)2⋅12FV = 5000 \left(1 + \frac{0.0345}{12}\right)^{2 \cdot 12}

Ensure your interest rate is in decimal form, and the compounding frequency (“c”) is correct. For monthly compounding, “c” would be 12. This will help you calculate the future value of your investment more accurately.

4. Finish the math computations in the formula. Start by solving the operations within parentheses first. This is known as the “order of operations” in mathematics.

• Divide the interest rate by the compounding frequency:

0.034512=0.00288\frac{0.0345}{12} = 0.00288

• Add this to 1:

1+0.00288=1.002881 + 0.00288 = 1.00288

Now, multiply the exponent by the number of periods: 2⋅12=242 \cdot 12 = 24

• Raise the value inside the parentheses to the power of 24:

1.0028824=1.07151.00288^{24} = 1.0715

Finally, multiply the result by the principal ($5,000): FV=5000⋅1.0715=5357.50FV = 5000 \cdot 1.0715 = 5357.50

Your future value is $5,357.50 after 2 years.

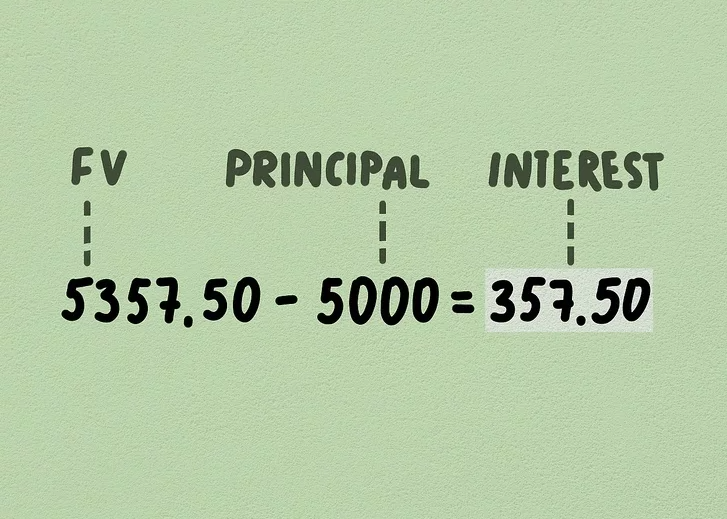
5. Subtract the principal from the future value. To calculate the total interest earned, subtract the original principal from the future value. 5357.50−5000=357.505357.50 – 5000 = 357.50

So, in this example, you will earn $357.50 in interest over the 2-year period. This shows how compound interest significantly increases the value of your investment over time.

For more on compound interest and how to calculate it, you can refer to Investopedia’s detailed guide.

Part3

Calculating Compound Interest with Regular Payments

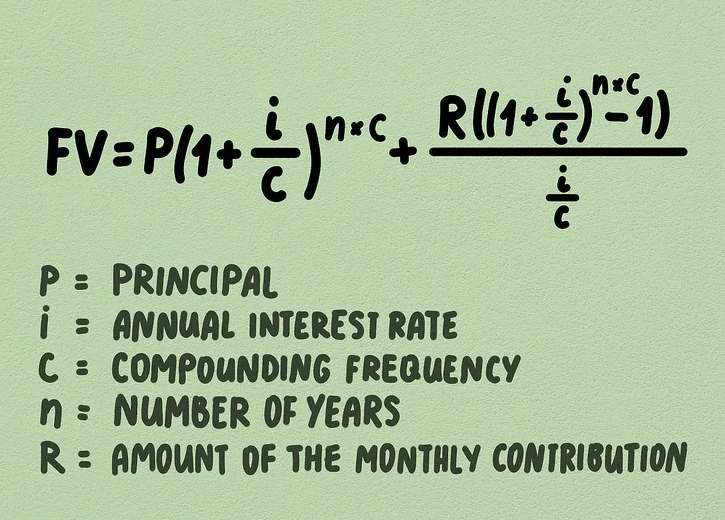
1. Learn the formula. Compound interest accounts can grow even faster when you make regular contributions, such as adding a fixed monthly amount to a savings account. While the formula for compound interest with regular payments is longer than the one used for simple compound interest, it follows the same basic principles. The formula for calculating the future value of an investment with regular contributions is: FV=P(1+ic)n⋅c+R((1+ic)n⋅c−1)icFV = P \left(1 + \frac{i}{c}\right)^{n \cdot c} + \frac{R \left( \left(1 + \frac{i}{c}\right)^{n \cdot c} – 1 \right)}{\frac{i}{c}}

Where:

• “FV” is the future value of the investment.
• “P” is the principal (initial investment).
• “i” is the annual interest rate.
• “c” is the compounding frequency (how often interest is compounded).
• “n” is the number of years.
• “R” is the amount of the monthly contribution.

For more information on this formula, check out Investopedia’s guide on compound interest.

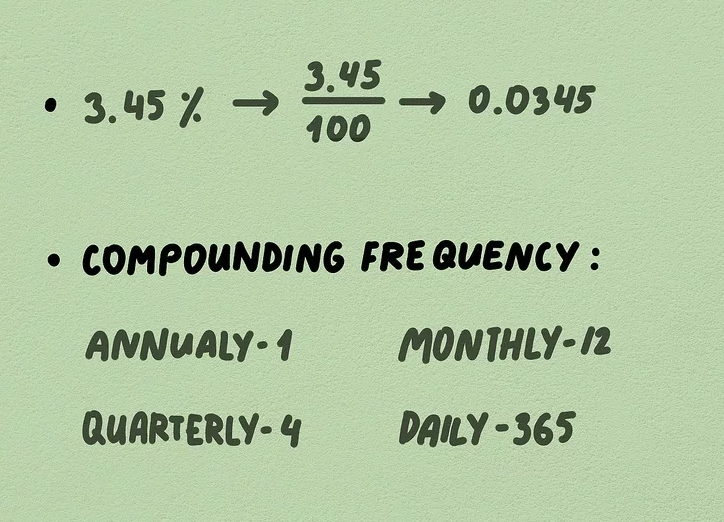
2. Compile the necessary variables. To calculate the future value of an account with regular contributions, gather the following information:

• The principal amount of the account.
• The annual interest rate (convert it to a decimal by dividing by 100).
• The compounding frequency, which could be annually, monthly, or daily. For example, monthly compounding would have a frequency of 12.
• The number of years for the investment.
• The monthly contribution amount.

For instance, if your principal is $5,000, your annual interest rate is 3.45%, you are making monthly contributions of $100, and the account compounds monthly, you’ll need to use these values in the formula.

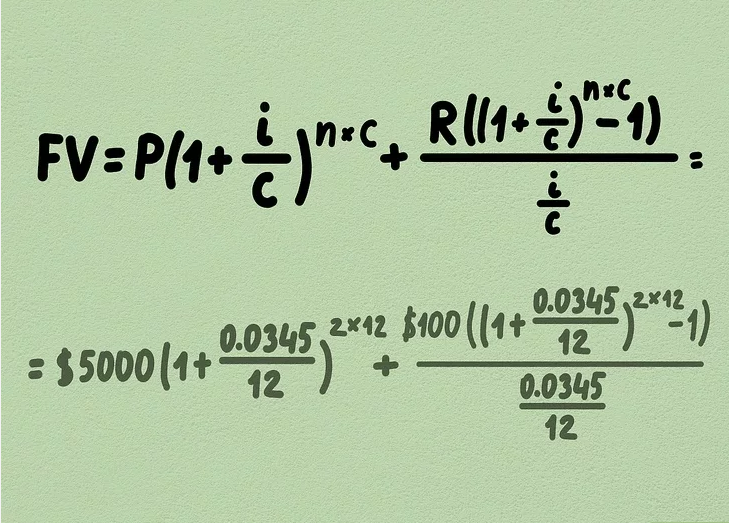
3. Input your variables. Using the information from the previous step, the formula to calculate the future value would look like this: FV=5000(1+0.034512)2⋅12+100((1+0.034512)2⋅12−1)0.034512FV = 5000 \left(1 + \frac{0.0345}{12}\right)^{2 \cdot 12} + \frac{100 \left( \left(1 + \frac{0.0345}{12}\right)^{2 \cdot 12} – 1 \right)}{\frac{0.0345}{12}}

Here, the principal amount is $5,000, the interest rate is 3.45%, the account compounds monthly, and the monthly contribution is $100 over a period of 2 years.

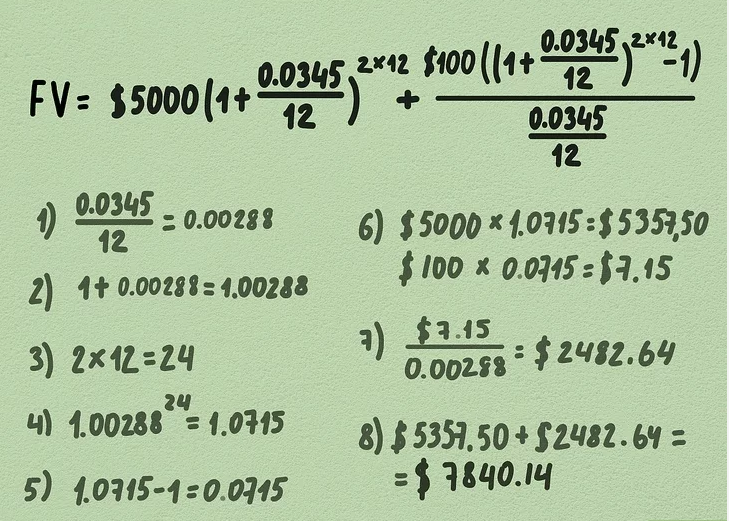
4. Solve the equation. To solve the formula, follow the order of operations:

1. Start by calculating the fraction inside the parentheses: 0.034512=0.00288\frac{0.0345}{12} = 0.00288.
2. Add 1 to this result: 1+0.00288=1.002881 + 0.00288 = 1.00288.
3. Multiply the number of years by the compounding frequency: 2×12=242 \times 12 = 24.
4. Raise 1.002881.00288 to the power of 24: 1.0028824=1.07151.00288^{24} = 1.0715.
5. Multiply the principal by 1.07151.0715: 5000×1.0715=5357.505000 \times 1.0715 = 5357.50.
6. Subtract 1 from the exponent result: 1.0715−1=0.07151.0715 – 1 = 0.0715.
7. Multiply the monthly contribution by 0.07150.0715: 100×0.0715=7.15100 \times 0.0715 = 7.15.
8. Divide by the fraction 0.034512=0.00288\frac{0.0345}{12} = 0.00288: 7.150.00288=2482.64\frac{7.15}{0.00288} = 2482.64.
9. Add the results: 5357.50+2482.64=7840.145357.50 + 2482.64 = 7840.14.

The future value of the account after 2 years is $7,840.14.

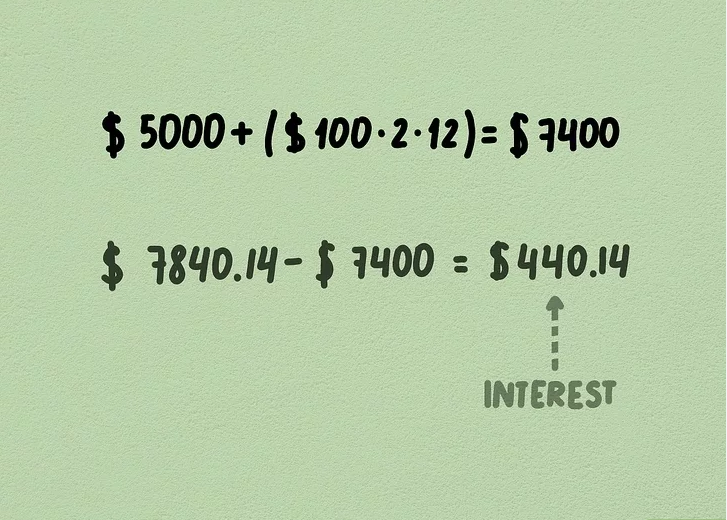
5. Subtract the principal and payments. To find the total interest earned, subtract the amount of money you contributed to the account. In this case, you contributed $5,000 as the principal and $2,400 in monthly payments ($100 × 24 months).

The total contributions are $5,000 + $2,400 = $7,400. Subtracting this from the future value of $7,840.14 gives you: 7,840.14−7,400=440.147,840.14 – 7,400 = 440.14

So, you earned $440.14 in interest over the 2 years.

6. Extend your calculation. To see the full potential of compound interest, imagine continuing to add $100 per month for 20 years instead of just 2. In this case, your future value would be approximately $45,000, with total contributions of $29,000. This means you would earn $16,000 in interest over the 20-year period.

For further information on the benefits of compound interest and how it grows over time, visit Investopedia’s guide on compound interest.